仭僩僢僾儁乕僕
仭嶼悢丒悢妛僗乕僷乕屄暿巜摫偺偛埬撪
仭撳拞妛嶼悢擖帋栤戣
仭偍傕偟傠嶼悢栤戣丂俆侽栤乮拞妛擖帋乯
仭拞妛庴尡嶼悢傪妝偟偔嬌傔偨偄乮僽儘僌)
仭嶼悢僀儀儞僩側偳偺幨恀
仭嵟嬤峴偭偨強
仭偍栤偄崌傢偣
偙偺壓偵懕偔偍傕偟傠嶼悢栤戣偺拞偐傜
偁側偨偺偍婥偵擖傝偺栤戣偑傂偲偮偱傕尒偮偐傞偲偄偄偱偡偹
帺暘偺摢偱峫偊傞婌傃傪枴傢偭偰傒偰偔偩偝偄
夝偗偨弖娫偺姶摦偺婌傃傪偁側偨傕枴傢偭偰傒偰乣乣偦傟偱偼丄偛備偭偔傝偳偆偧
俀侽俀俀擭搙丂杻晍拞妛丂嶼悢丂俁斣 惍悢丂応崌偺悢丂俁偺攞悢 師偺忦審偵摉偰偼傑傞係寘偺惍悢傪峫偊傑偡丅 忦審丂丗丂侾偮偺悢帤傪俁屄丄暿偺悢帤傪侾屄暲傋偰嶌傜傟傞丅 椺偊偽丄俀侽俀俀偼偙偺忦審偵摉偰偼傑偭偰偄傑偡丅 埲壓偺栤偄偵摎偊側偝偄丅 乮侾乯 忦審偵摉偰偼傑傞係寘偺惍悢偺偆偪丄 偳偺寘偺悢帤傕侽偱側偄傕偺偼偄偔偮偁傝傑偡偐丅 乮俀乯丂忦審偵摉偰偼傑傞係寘偺惍悢偼慡晹偱偄偔偮偁傝傑偡偐丅 乮俁乯丂忦審偵摉偰偼傑傞係寘偺惍悢偺偆偪丄 俁偺攞悢偱偁傞傕偺偼偄偔偮偁傝傑偡偐丅 夝偒曽丂 乮1乯丂係亊俋亊俉亖俀俉俉丂 乮俀乯丂係亊俋亊俉亄乮俁亊俋亄俋乯亖俋亊俁俇亖俁俀係 乮俁乯丂係亊俋亊俉亊乮侾乛俁乯亄俁亊俋亄俋亊乮侾乛俁乯亖侾俀俇 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂乮1乯丂俀俉俉丂乮俀乯丂俁俀係丂乮俁乯丂侾俀俇 |
撳拞妛丂擖帋栤戣丂俀侽侾俋擭搙丂乮丂暯惉俁侾擭搙丂乯擖帋 嶼悢侾擔栚丂俇斣丂攞悢丂戝偒側慺悢丂帋峴嶖岆丂幚尡丂 俉俋偺攞悢偲侾侾俁偺攞悢傪丄 俉俋丆侾侾俁丆侾俈俉丆俀俀俇丆丒丒丒丒丒丒丒丒 偺傛偆偵彫偝偄傕偺偐傜弴偵暲傋傞偲偒丄 俆侽斣栚偺悢偼丂仩丂偱偡丅 夝偒曽侾丂戝偞偭傁朄偱偄偒傑偡 傎偲傫偳寁嶼偟側偄偱摎偊偑弌偣傞婥帩偪傛偝丄姶妎偑丄 偁側偨偵傕揱傢傟偽偆傟偟偄偱偡 俉俋傕侾侾俁傕慺悢偱偁傞偙偲偵拲堄偡傞 俉俋偲侾侾俁偺斾偼俉俉丗侾侾俀亖侾侾丗侾係偵嬤偄偲峫偊傑偡 偙偙偱侾侾亄侾係亖俀俆偱偁傞偙偲偵婥偯偔偲儔僢僉乕偱偡 栤戣暥偺俆侽斣栚偺俆侽偼俀俆偺俀攞偱偡偐傜丄 俉俉亊俀俉偲侾侾俀亊俀俀偺妡偗嶼偺寢壥俀係俇係偼弌偝側偔偰傕 俉俉偺攞悢偺俀俉斣栚偲侾侾俀偺攞悢偺俀俀斣栚偼摨偠偱偡 俉俉亊俀俉亖侾侾俀亊俀俀偱偡 俉俋亊俀俉偼俉俉亊俀俉傛傝俀俉戝偒偄 侾侾俁亊俀俀偼侾侾俀亊俀俀傛傝俀俀戝偒偄 偙偲偵婥傪偮偗傟偽丄 俉俋亊俀俉偑彫偝偄曽偐傜俆侽斣栚偩偲暘偐傝傑偡 慄暘恾傪彂偄偰偁偘傞偲棟夝偟傗偡偄偐傕偱偡 俉俋亊俀俉亖乮俋侽亅侾乯亊俀俉亖俀俆俀侽亅俀俉亖俀係俋俀 夝偒曽 俀丂俆侽屄傪俀俆屄偢偮偵暘偗偰傒偰偐傜丄挷惍偡傞 俉俋偺攞悢偺俀俆斣栚偲侾侾俁偺攞悢偺俀俆斣栚偺嵎偼 俀係亊俀俆亖俇侽侽偱偡 俇侽侽偺嵎傪堄幆偟偰 俉俋偺攞悢傪俁屄憹傗偟侾侾俁偺攞悢傪俁屄尭傜偡偲 乮俉俋亄侾侾俁乯亊俁亖俇侽俇 傛偭偰俉俋亊俀俉偑俆侽斣栚偲暘偐傞 俉俋亊俀俉亖乮俋侽亅侾乯亊俀俉亖俀俆俀侽亅俀俉亖俀係俋俀 夝偒曽 俁丂彫偝偄弴偵俈屄偱嵎偑侾俈偵婥偯偔 俉俋亊係亖俁俆俇 侾侾俁亊俁亖俁俁俋 嵎偑侾俈側偺偱丄偙傟傪俈僙僢僩 俉俋亊俀俉偼侾侾俁亊俀侾傛傝侾侾俋戝偒偄偺偱 侾侾俁傪侾屄捛壛偡傞偲 俉俋亊俀俉偼侾侾俁亊俀俀傛傝俇戝偒偄偙偲偵側傞 傛偭偰丄俉俋亊俀俉亖俀係俋俀 夝偒曽 係丂彫偝偄弴偵俋屄偱嵎偑俈偵婥偯偔 俉俋偺攞悢丂 89 178 267 356 445丒丒丒丒丒丒 侾侾俁偺攞悢丂113 226 339 452丒丒丒丒丒丒 89丂丂113丂 178丂226丂 267丂 339丂 356丂 445丂 452 彫偝偄弴偵暲傋傞偲俉俋偺攞悢偲侾侾俁偺攞悢偑岎屳偵弌偰偒傑偡偑丄 俈斣栚偲俉斣栚偑楢懕偟偰俉俋偺攞悢偑弌偰偔傞 俉斣栚偲俋斣栚偺嵎偑俀係亊係亅俉俋亖俈 俉俋亊俆亖係係俆 侾侾俁亊係亖係俆俀 嵎偑俈偱丄偙傟傪俆僙僢僩 侾侾俁亊俀侽偼俉俋亊俀俆傛傝俁俆戝偒偄 俁俆戝偒偄偙偲傪堄幆偟偰丄巆傝俆屄傪 俉俋偺攞悢俁屄丄侾侾俁偺攞悢俀屄捛壛偡傞偲 俆侽斣栚偼俉俋偺攞悢偺俀俉屄栚偱 侾侾俁偺攞悢偺俀俀屄栚傛傝俇戝偒偔側傞 傛偭偰丄俉俋亊俀俉亖俀係俋俀 妝偟傫偱偄偨偩偗傑偟偨偱偟傚偆偐 摎偊丂俀係俋俀 |
俀侽俀俀擭搙丂惔晽撿奀拞妛丂嶼悢丂俀斣丂乮俁乯丂 惍悢丂応崌偺悢丂 乮俁乯丂偳偙偐偺埵偵彮側偔偲傕侾偮俁偑偁傞惍悢傪峫偊傑偡丅 嘆丂侾偐傜侾侽侽傑偱偺側偐偵丄偙偺傛偆側惍悢偼壗屄偁傝傑偡偐丅 嘇丂侾偐傜侾侽侽侽傑偱偺側偐偵丄偙偺傛偆側惍悢偼壗屄偁傝傑偡偐丅 夝偒曽丂 嘆丂10俀乗俋俀亖19 嘇丂10俁乗俋俁亖271 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂嘆丂侾俋丂嘇丂俀俈侾 |
俀侽俀俀擭搙丂堦嫶戝妛丂悢妛丂侾斣丂惍悢丂懳徧惈 慺場悢暘夝丂慺悢丂榑棟丂応崌暘偗丂崌摨幃丂嬼婏惈 俀a俁倐亄 俀c俁倓亖俀侽俀俀丂傪枮偨偡 侽埲忋偺惍悢丂a,丂b,丂c,丂d丂偺慻傪媮傔傛丅 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂乮丂a ,b ,c ,d丂乯亖乮侾丆俆丆俋丆侾乯丆乮俋丆侾丆侾丆俆乯 |
俀侽俀俀擭搙丂撳崅峑丂悢妛丂係斣 妋棪丂応崌偺悢丂応崌暘偗 A丆P丆S偺俁庬椶偺暥帤偐傜柍嶌堊偵侾暥帤傪慖傇偙偲傪孞傝曉偟峴偄丄 慖傫偩暥帤傪慖傫偩弴斣偵嵍偐傜塃偵岦偐偭偰侾楍偵暲傋偰偄偔丅 乮侾乯 暥帤傪俇屄暲傋偨偲偒丄 乽PASS乿偲偄偆楢懕偟偨暥帤偺暲傃偑娷傑傟傞妋棪傪媮傔傛丅 乮俀乯 暥帤傪俋屄暲傋偨偲偒丄 乽PASS乿偲偄偆楢懕偟偨暥帤偺暲傃偑娷傑傟傞妋棪傪媮傔傛丅 夝偒曽丂 乮侾乯丂 PASS仜仜 仜PASS仜 仜仜PASS 偺俁僷僞乕儞 乮俁俀亊俁乯/ 俁俇亖侾/俀俈 乮俀乯 傾丂PASS仜仜仜仜仜 僀丂仜PASS仜仜仜仜 僂丂仜仜PASS仜仜仜 僄丂仜仜仜PASS仜仜 僆丂仜仜仜仜PASS仜 僇丂仜仜仜仜仜PASS PASSPASS仜丂偑傾偲僆 PASS仜PASS丂偑傾偲僇 仜PASSPASS丂偑僀偲僇 偱俀夞悢偊傜傟偰偄傞偙偲偵婥傪偮偗偰 乮俁俆亊俇乗俁亊俁乯/ 俁俋亖侾俇侾/俀侾俉俈 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂乮1乯丂1乛俀俈丂乮俀乯丂侾俇侾/俀侾俉俈 |
俀侽俀俀擭搙丂拀攇戝妛晬懏嬵応崅峑丂悢妛丂俀斣 惍悢丂慺場悢暘夝 暘曣偑俀俀俀偱偁傝丄暘巕偑俀俀俀埲壓偺惓偺惍悢偱偁傞暘悢偵偮偄偰峫偊傑偡丅 偙傟傜偺暘悢偺偆偪丄暘曣偲暘巕偑侾埲奜偺岞栺悢傪傕偮傕偺偡傋偰傪丄 師偺傛偆偵彫偝偄弴偵暲傋傑偡丅 俀/俀俀俀丆俁/俀俀俀丆係/俀俀俀丆俇/俀俀俀丆丒丒丒丆俀俀侽/俀俀俀丆俀俀俀/俀俀俀 暲傋偨暘悢偵偮偄偰丄師偺栤偄偵摎偊側偝偄丅 乮侾乯 暲傋偨暘悢偺屄悢傪媮傔側偝偄 乮俀乯丂暲傋偨暘悢偺偡傋偰偺榓 俀/俀俀俀亄俁/俀俀俀亄係/俀俀俀亄俇/俀俀俀亄丒丒丒亄俀俀侽/俀俀俀亄俀俀俀/俀俀俀 傪媮傔側偝偄丅 乮俁乯丂暲傋偨暘悢偺偡傋偰偺愊 俀/俀俀俀亊俁/俀俀俀亊係/俀俀俀亊俇/俀俀俀亊丒丒丒亊俀俀侽/俀俀俀亊俀俀俀/俀俀俀 傪丄惓偺惍悢M丆N偱丂N乛M偲昞偟傑偡丅 偨偩偟丄M偲N偺嵟戝岞栺悢偼侾偱偡丅 M傪慺場悢暘夝偟偨寢壥傪丄椵忔偺巜悢傪巊偭偰昞偟側偝偄丅 夝偒曽丂 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂乮1乯丂侾俆侽丂乮俀乯丂侾俆侾/俀丂乮俁乯丂M亖俁係俀亊俁俈侾係係 |
偍傕偟傠嶼悢栤戣丂俆侽丂乮丂棇撿崅峑晬懏拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俋丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俉丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俈丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俇丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俆丂乮丂搶戝帥妛墍拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係係丂乮丂峛梲妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俁丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係俀丂乮丂戝嶃惎岝妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係侾丂乮丂巐揤墹帥拞丂乯丂偵僠儍儗儞僕丂丱丱丟
俀侽俀俀擭搙丂奐惉拞妛丂嶼悢丂侾斣丂乮俁乯丂 応崌偺悢丂僒僀僐儘係偮偺弌偨栚偺愊丂係偺攞悢丂 乮俁乯丂係恖偺恖偑僒僀僐儘傪侾夞偢偮傆傞偲偒丄 栚偺弌曽偼慡晹偱俇亊俇亊俇亊俇亖侾俀俋俇捠傝偁傝傑偡丅 偙偺拞偱丄係偮偺弌偨栚偺悢傪偡傋偰偐偗傞偲 係偺攞悢偵側傞栚偺弌曽偼壗捠傝偁傝傑偡偐丅 夝偒曽丂俇係乕俁係乕係亊俀亊俁俁亖俋俋俋 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂俋俋俋 |
偍傕偟傠嶼悢栤戣丂係侽丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁俋丂乮丂戝嶃惎岝妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟丂
偍傕偟傠嶼悢栤戣丂俁俉丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟丂
偍傕偟傠嶼悢栤戣丂俁俈丂乮丂峛梲妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁俇丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁俆丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁係丂乮丂棇撿崅峑晬懏拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁俁丂乮丂峛梲妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁俀丂乮丂棇撿崅峑晬懏拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俁侾丂乮丂棇撿崅峑晬懏拞丂乯丂偵僠儍儗儞僕丂丱丱丟
俀侽俀俀擭搙丂嬵応搶朚拞妛丂丂嶼悢丂侾斣丂乮俀乯丂 惍悢丂応崌偺悢丂慻崌偣丂 乮俀乯丂侾埲忋俀侽俀俀埲壓偺惍悢偺偆偪丄 奺埵偺悢帤偺榓偑俇偱偁傞惍悢偼壗屄偁傝傑偡偐丅 夝偒曽丂俀俉亄俀侾亄俁亖俆俀 夝偒曽俀丂俉係亅俁俆亄俁亖俆俀 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂俆俀 |
偍傕偟傠嶼悢栤戣丂俁侽丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俋丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俉丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俈丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俇丂乮丂峛梲妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俆丂乮丂峛梲妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀係丂乮丂戝嶃惎岝妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀俁丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟丂
偍傕偟傠嶼悢栤戣丂俀俀丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俀侾丂乮丂巐揤墹帥拞丂乯丂偵僠儍儗儞僕丂丱丱丟
撳拞妛丂擖帋栤戣丂俀侽俀俀擭搙丂乮丂椷榓係擭搙丂乯擖帋 嶼悢侾擔栚丂係斣 惍悢丂梋傝丂崌摨幃丂2偺椵忔乮傋偒忔乯丂丂丂 俀傪侾侽屄偐偗偰偱偒傞悢 俀亊俀亊俀亊俀亊俀亊俀亊俀亊俀亊俀亊俀傪 侾俈偱妱偭偨梋傝偼丂仩丂偱偡丅 傑偨丄俀傪俀侽俀俀屄偐偗偰偱偒傞悢 俀亊丒丒丒丒丒丒丒丒丒亊俀傪 侾俈偱妱偭偨梋傝偼丂仩丂偱偡丅 夝偒曽 慜敿丂丂侾亊俀亊俀亖係 屻敿丂丂侾俈乕俀亊俀亖侾俁 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎偊丂弴偵丂係丂丂侾俁 |
偍傕偟傠嶼悢栤戣丂俀侽丂乮丂撳拞丂乯丂偵僠儍儗儞僕丂丱丱丟丂
偍傕偟傠嶼悢栤戣丂侾俋丂乮丂搶戝帥妛墍拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俉丂乮丂搶戝帥妛墍拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俈丂乮丂搶戝帥妛墍拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俇丂乮丂搶戝帥妛墍拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俆丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾係丂乮丂棇撿崅峑晬懏拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俁丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾俀丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂侾侾丂乮丂棇惎拞丂乯丂偵僠儍儗儞僕丂丱丱丟
俀侽俀俀擭搙丂拀攇戝妛晬懏嬵応拞妛丂嶼悢丂侾斣 惍悢丂楢懕惍悢偺榓偑俀侽俀俀丂婏悢偺栺悢偺屄悢 摍嵎悢楍偺榓偺岞幃丂嬼婏惈丂嶰妏悢丂慺場悢暘夝丂 偁傞惍悢傪丄俀屄埲忋偺楢懕偟偨惍悢偺榓偱昞偡偙偲傪峫偊傑偡丅 偙偙偱偼丄惍悢仜偐傜惍悢仮傑偱偺 楢懕偟偨惍悢偺榓傪亙仜乣仮亜偲彂偔偙偲偵偟傑偡丅 偨偲偊偽丄俋亖俀亄俁亄係側偺偱丄俋偼丂亙俀乣係亜偱昞偣傑偡丅 俋傪俀屄埲忋偺楢懕偟偨惍悢偺榓偱昞偡偲偒丄 峫偊傜傟傞昞偟曽偼丂亙俀乣係亜偲亙係乣俆亜偺偪傚偆偳俀庬椶偱偡丅 師偺乮侾乯偐傜乮俁乯偺惍悢傪丅俀屄埲忋偺楢懕偟偨惍悢偺榓偱 偦傟偧傟昞偡偲偒丄峫偊傜傟傞昞偟曽傪 亙仜乣仮亜偺傛偆偵偟偰偡傋偰摎偊側偝偄丅 乮侾乯 俆侽 乮俀乯侾侽侽侽 乮俁乯俀侽俀俀 夝偒曽丂 慺場悢暘夝偡傞丅 偦偟偰丄侾傛傝戝偒偄婏悢偺栺悢偵偮偄偰挷傋傞 乮侾乯 俆侽亖俀亊俆亊俆 婏悢偺栺悢偼俆偲俀俆 乮俀乯侾侽侽侽亖俀亊俀亊俀亊俆亊俆亊俆 婏悢偺栺悢偼俆偲俀俆偲侾俀俆 乮俁乯俀侽俀俀亖俀亊俁亊俁俁俈 婏悢偺栺悢偼俁偲俁俁俈偲侾侽侾侾 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂乮1乯丂亙俉乣侾俀亜丂亙侾侾乣侾係亜 乮俀乯丂亙俀俉乣俆俀亜丂亙俆俆乣俈侽亜丂亙侾俋俉乣俀侽俀亜 乮俁乯丂亙侾俇俁乣侾俈係亜丂亙俆侽係乣俆侽俈亜丂亙俇俈俁乣俇俈俆亜丂 |
偍傕偟傠嶼悢栤戣丂侾侽丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俋丂乮丂恄屗彈妛堾拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俉丂乮丂擔杮彈巕戝晬拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俈丂乮丂撨恵崅尨奀忛拞丂乯丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俇丂乮撳拞妛乯偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂俆丂偵僠儍儗儞僕丂丱丱丟
偍傕偟傠嶼悢栤戣丂係丂偵僠儍儗儞僕丂丱丱丟丂丂
偍傕偟傠嶼悢栤戣丂3丂偵僠儍儗儞僕丂丱丱丟丂丂
偍傕偟傠嶼悢栤戣丂2丂乮惔晽拞丂屻婜乯偵僠儍儗儞僕丂丱丱丟丂
偍傕偟傠嶼悢栤戣丂1丂乮峛梲妛堾拞乯偵僠儍儗儞僕丂丱丱丟丂
俀侽俀俀擭搙丂媣棷暷戝妛晬愝拞妛丂嶼悢丂侾斣丂乮俀乯丂 応崌偺悢丂 乮俀乯丂乽侾乿偑俀枃丄乽俀乿偑俀枃丄乽俁乿偑侾枃丄 崌寁俆枃偺僇乕僪偑偁傝傑偡丅 偙偺拞偐傜俁枃偲偭偰側傜傋偰偱偒傞俁偗偨偺惍悢偼 慡晹偱壗庬椶偁傝傑偡偐丅 夝偒曽丂俁俁乗乮俁亄俁亊俀乯亖侾俉 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂侾俉 |
丂拞妛庴尡嶼悢偺寁嶼丂(彈巕妛堾拞乯偵僠儍儗儞僕丂丱丱丟
俀侽侾俇擭搙丂峛梲妛堾拞妛丂嶼悢丂俀擔栚侾斣丂乮侾乯 師偺仩偺拞偵揔摉側悢傪擖傟側偝偄丅 俇俈俉俋亊俇俈俉俋亊俇俈俉俋亅俇俈俉俉亊俇俈俉俋亊俇俈俋侽亖仩 夝偒曽 偁傢偰偰寁嶼偟偩偟偨傜偩傔偱偡傛乕 傛偔尒偨傜俇俈俉俋偱傑偲傔傜傟傑偡偹 俇俈俉俋亊乮俇俈俉俋亊俇俈俉俋亅俇俈俉俉亊俇俈俋侽乯 亖俇俈俉俋 嶼悢戝岲偒側彫妛惗偺偍巕條偲 弌夛偊傞偺傪妝偟傒偵偍懸偪偟偰偍傝傑偡 嫽枴偺偁傞曽偼丄偍婥寉偵楢棈傪両 |
俀侽侾俋擭搙丂搶戝帥妛墍拞妛丂嶼悢丂侾斣丂乮侾乯 師偺仩偵摉偰偼傑傞悢傪媮傔側偝偄丅 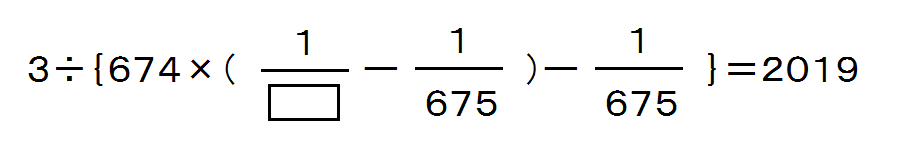 摎偊偼偡偖偵弌偣傞偲巚偄傑偡偑丄 摎偊偵偄偨傞搑拞夁掱傪岺晇偡傞偲 偁側偨偩偗偺僆儕僕僫儖側寁嶼曽朄偑敪尒偝傟傞偙偲傕偁傝 傎偐偺栤戣偵傕偦偺摨偠寁嶼曽朄偑巊偊偰 偳傫偳傫妝偟偔側傝傑偡傛 摎丂丂俇俈俁 |
俀侽俀俀亖俁俁俈亊俀亊俁 俁俁俈偼慺悢偱偡 俁俁俈偼慺悢偱偡 婏慺悢俁俁俈偼俀偮偺暯曽悢偺榓偱昞偝傟傞 |
俀侽俀俁擭搙拞妛庴尡梊掕偺曽傊 俀侽俀俁亖俈亊侾俈亊侾俈 俀侽俀俁偼慺悢偱偼偁傝傑偣傫 俈傗侾俈傗侾侾俋傗俀俉俋側偳偺攞悢偱偡 俀侽侽侽偐傜俀侾侽侽傑偱偺慺悢偼 俀侽侽俁丆俀侽侾侾丆俀侽侾俈丆俀侽俀俈丆俀侽俀俋丆 俀侽俁俋丆俀侽俆俁丆俀侽俇俁丆俀侽俇俋丆俀侽俉侾丆 俀侽俉俁丆俀侽俉俈丆俀侽俉俋丆俀侽俋俋偺侾係屄偁傝傑偡
|
偍傕偟傠嶼悢栤戣丂俆侽栤乮拞妛擖帋乯偵僠儍儗儞僕偼僐僠儔丂仺偍傕偟傠嶼悢栤戣丂俆侽栤乮拞妛擖帋乯
撳拞妛嶼悢擖帋栤戣夝愢偼僐僠儔丂仺丂撳拞妛嶼悢擖帋栤戣
俀侽俀俀擭拞妛擖帋梊憐栤戣偼僐僠儔丂仺俀侽俀俀擭拞妛擖帋梊憐栤戣
俀侽侾俈乮丂慺悢丂乯擭拞妛擖帋梊憐栤戣偼僐僠儔丂仺俀侽侾俈擭拞妛擖帋梊憐栤戣
偍傕偟傠嶼悢栤戣丂俀侽侾俇擭乮拞妛擖帋乯偵僠儍儗儞僕偼僐僠儔丂仺偍傕偟傠嶼悢栤戣丂俀侽侾俇擭乮拞妛擖帋乯
偍傕偟傠嶼悢栤戣丂俀侽侾俆擭乮拞妛擖帋乯偵僠儍儗儞僕偼僐僠儔丂仺偍傕偟傠嶼悢栤戣丂俀侽侾俆擭乮拞妛擖帋乯
俀侽俀俀擭拞妛擖帋梊憐栤戣偼僐僠儔丂仺俀侽俀俀擭拞妛擖帋梊憐栤戣
偍傕偟傠嶼悢栤戣丂俀侽俀俀擭乮拞妛擖帋乯偵僠儍儗儞僕偼僐僠儔丂仺偍傕偟傠嶼悢栤戣丂俀侽俀俀擭乮拞妛擖帋乯
仭僩僢僾儁乕僕
仭嶼悢丒悢妛僗乕僷乕屄暿巜摫偺偛埬撪
仭撳拞妛嶼悢擖帋栤戣
仭偍傕偟傠嶼悢栤戣丂俆侽栤乮拞妛擖帋乯
仭偍栤偄崌傢偣