■トップページ
■算数・数学スーパー個別指導のご案内
■灘中学算数入試問題
■おもしろ算数問題 50問(中学入試)
■中学受験算数を楽しく極めたい(ブログ)
■算数イベントなどの写真
■最近行った所
■お問い合わせ
この下に続くおもしろ算数問題の中から
あなたのお気に入りの問題がひとつでも見つかるといいですね
自分の頭で考える喜びを味わってみてください
解けた瞬間の感動の喜びをあなたも味わってみて~~それでは、ごゆっくりどうぞ
2022年度 筑波大学附属駒場高校 数学 2番 整数 素因数分解 分母が222であり、分子が222以下の正の整数である分数について考えます。 これらの分数のうち、分母と分子が1以外の公約数をもつものすべてを、 次のように小さい順に並べます。 2/222,3/222,4/222,6/222,・・・,220/222,222/222 並べた分数について、次の問いに答えなさい。 (1) 並べた分数の個数を求めなさい (2) 並べた分数のすべての和 2/222+3/222+4/222+6/222+・・・+220/222+222/222 を求めなさい。 (3) 並べた分数のすべての積 2/222×3/222×4/222×6/222×・・・×220/222×222/222 を、正の整数M,Nで N/Mと表します。 ただし、MとNの最大公約数は1です。 Mを素因数分解した結果を、累乗の指数を使って表しなさい。 解き方 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 150 (2) 151/2 (3) M=342×37144 |
2022年度 灘高校 数学 4番 確率 場合の数 場合分け A,P,Sの3種類の文字から無作為に1文字を選ぶことを繰り返し行い、 選んだ文字を選んだ順番に左から右に向かって1列に並べていく。 (1) 文字を6個並べたとき、 「PASS」という連続した文字の並びが含まれる確率を求めよ。 (2) 文字を9個並べたとき、 「PASS」という連続した文字の並びが含まれる確率を求めよ。 解き方 (1) PASS○○ ○PASS○ ○○PASS の3パターン (32×3)/ 36=1/27 (2) ア PASS○○○○○ イ ○PASS○○○○ ウ ○○PASS○○○ エ ○○○PASS○○ オ ○○○○PASS○ カ ○○○○○PASS PASSPASS○ がアとオ PASS○PASS がアとカ ○PASSPASS がイとカ で2回数えられていることに気をつけて (35×6―3×3)/ 39=161/2187 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 1/27 (2) 161/2187 |
2022年度 一橋大学 数学 1番 整数 対称性 素因数分解 素数 論理 場合分け 合同式 偶奇性 2a3b+ 2c3d=2022 を満たす 0以上の整数 a, b, c, d の組を求めよ。 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 ( a ,b ,c ,d )=(1,5,9,1),(9,1,1,5) |
2022年度 麻布中学 算数 3番 整数 場合の数 3の倍数 次の条件に当てはまる4桁の整数を考えます。 条件 : 1つの数字を3個、別の数字を1個並べて作られる。 例えば、2022はこの条件に当てはまっています。 以下の問いに答えなさい。 (1) 条件に当てはまる4桁の整数のうち、 どの桁の数字も0でないものはいくつありますか。 (2) 条件に当てはまる4桁の整数は全部でいくつありますか。 (3) 条件に当てはまる4桁の整数のうち、 3の倍数であるものはいくつありますか。 解き方 (1) 4×9×8=288 (2) 4×9×8+(3×9+9)=9×36=324 (3) 4×9×8×(1/3)+3×9+9×(1/3)=126 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 288 (2) 324 (3) 126 |
2022年度 清風南海中学 算数 2番 (3) 整数 場合の数 (3) どこかの位に少なくとも1つ3がある整数を考えます。 ① 1から100までのなかに、このような整数は何個ありますか。 ② 1から1000までのなかに、このような整数は何個ありますか。 解き方 ① 102―92=19 ② 103―93=271 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 ① 19 ② 271 |
2022年度 渋谷教育学園渋谷中学 算数 2番 整数 場合の数 倍数 1,2,3,4,5の5つの数字だけを使ってできる4桁の数すべてを 次のように小さい順に並べました。 1111,1112,1113,1114,1115,1121,1122,・・・・,5553,5554,5555 次の問いに答えなさい。 (1) 全部で何個並んでいますか。 (2) 8の倍数は何個並んでいますか。 (3) 並んでいる数をすべてかけあわせました。 その積は一の位から0が何個続いていますか。 解き方 (1) 54=625 (2) (3×3+2×2)×5=65 (3) 5×1+3×4+2×20+1×100=157 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 625 (2) 65 (3) 157 |
2022年度 聖光学院中学 算数 2番 整数 場合の数 各位の数の和が各位の数の積以上である3桁の整数Aを考えます。 たとえば、925の各位の数の和は9+2+5=16、 各位の数の積は9×2×5=90となり、 925は整数Aとしてふさわしくありません。 このとき、次の問いに答えなさい。 (1) 百の位の数が9である整数Aは全部で何個ありますか。 (2) 3つの位の数の中に0を含む整数Aは全部で何個ありますか。 (3) 次の3つの条件すべてにあてはまる整数Aは全部で何個ありますか。 ・3つの位の数の中に0はない。 ・百の位の数は十の位の数以上である。 ・十の位の数は一の位の数以上である。 (4)整数Aは全部で何個ありますか。 解き方 (1) 9×2+1+1=20 (2) 19×9=171 (3) 9+1+1=11 (4) 171+1+3×8+3+6=205 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 20 (2) 171 (3) 11 (4) 205 |
2022年度 筑波大学附属駒場中学 算数 1番 整数 連続整数の和が2022 奇数の約数の個数 等差数列の和の公式 偶奇性 三角数 素因数分解 ある整数を、2個以上の連続した整数の和で表すことを考えます。 ここでは、整数○から整数△までの 連続した整数の和を<○~△>と書くことにします。 たとえば、9=2+3+4なので、9は <2~4>で表せます。 9を2個以上の連続した整数の和で表すとき、 考えられる表し方は <2~4>と<4~5>のちょうど2種類です。 次の(1)から(3)の整数を。2個以上の連続した整数の和で それぞれ表すとき、考えられる表し方を <○~△>のようにしてすべて答えなさい。 (1) 50 (2)1000 (3)2022 解き方 素因数分解する。 そして、1より大きい奇数の約数について調べる (1) 50=2×5×5 奇数の約数は5と25 (2)1000=2×2×2×5×5×5 奇数の約数は5と25と125 (3)2022=2×3×337 奇数の約数は3と337と1011 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) <8~12> <11~14> (2) <28~52> <55~70> <198~202> (3) <163~174> <504~507> <673~675> |
2022年度 開成中学 算数 1番 (3) 場合の数 サイコロ4つの出た目の積 4の倍数 (3) 4人の人がサイコロを1回ずつふるとき、 目の出方は全部で6×6×6×6=1296通りあります。 この中で、4つの出た目の数をすべてかけると 4の倍数になる目の出方は何通りありますか。 解き方 64ー34ー4×2×33=999 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 999 |
2022年度 開成中学 算数 1番 (2) 整数 計算 9で割った余り 九去法 合同式 (2) 次の計算の結果を9で割ったときの余りを求めなさい。 1234567+2345671+3456712 +4567123+5671234 解き方 1×5=5 1+2+3+4+5+6+7≡1 ( mod 9 ) (1+2+3+4+5+6+7)×5≡1×5≡5 ( mod 9 ) 解き方2 4×7×5≡20×7≡2×7≡5 ( mod 9 ) 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 5 |
2022年度 久留米大学附設中学 算数 1番 (2) 場合の数 (2) 「1」が2枚、「2」が2枚、「3」が1枚、 合計5枚のカードがあります。 この中から3枚とってならべてできる3けたの整数は 全部で何種類ありますか。 解き方 33―(3+3×2)=18 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 18 |
2022年度 駒場東邦中学 算数 1番 (2) 整数 場合の数 組合せ (2) 1以上2022以下の整数のうち、 各位の数字の和が6である整数は何個ありますか。 解き方 28+21+3=52 解き方2 84-35+3=52 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 52 |
2022年度 大阪星光学院中学 算数 1番 (2) 整数 場合の数 順列 (2) 1から6までの数字を1個ずつ使って6けたの数を作るとき、 521346は小さい方から数えて □ 番目の数です。 解き方 5!×4+4!+1=505 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 505 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 4番 整数 余り 合同式 2の累乗(べき乗) 2を10個かけてできる数 2×2×2×2×2×2×2×2×2×2を 17で割った余りは □ です。 また、2を2022個かけてできる数 2×・・・・・・・・・×2を 17で割った余りは □ です。 解き方 前半 1×2×2=4 後半 17ー2×2=13 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答え 順に 4 13 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 5番 整数 場合の数 偶奇性 式の扱い 分配法則 余事象 A、B、C、Dは1以上10以下の整数です。 A、B、C、Dの中に同じ整数が含まれていてもよいものとします。 A×B+A×C+A×D+B×C×Dが偶数となるような A、B、C、Dの組は全部で □ 組あります。 解き方 A、B、C、D の偶数、奇数で場合分けする 104 ― (5×53+5×53×3)=7500 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答え 7500 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 1番 計算 逆算 通分 方程式 分数 素因数分解  解き方 726=121×6 726=22×33 726=3×242 (□+33)×5=4×(242―42) □=4×200÷5-33=127 答え 127 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 2番 式の扱い 方程式 整数 仕事算 比 逆比 ある仕事に兄と弟が取り組みます。 兄は30分働くごとに5分休むことを繰り返します。 弟は働き始めると休まずに働き続けます。 兄が働き始め、その95分後に弟も一緒に働き始めると、 兄が働き始めてから135分後にこの仕事が終わります。 また、弟が働き始め、その90分後に兄も一緒に働き始めると、 弟が働き始めてから、140分後にこの仕事が終わります。 この仕事を弟だけで終わらせるには □ 分かかります。 解き方 [ 30 ]×4+<40>=<140>+[ 30 ]+[ 15 ] [ 75 ]=<100> [ 3 ]=<4> [ 120 ]+<40>=<160>+<40>=<200> 答え 200 |
灘中学 入試問題 2022年度 ( 令和4年度 )入試 算数1日目 3番 食塩水 濃度 てんびん算 逆比 濃度が □ %の食塩水が □ g 入っている容器に、 濃度が1.9%の食塩水100gを加えてよくかき混ぜると、 濃度が3.1%になりました。 そのあとに食塩10gを加えてよくかき混ぜると、 濃度が5%になりました。 解き方 てんびん図をかく (100-5)×10÷(5-3.1)=500 500-100=400 3.1+(3.1-1.9)÷4=3.4 答え 順に 3.4 400 |
灘中学 入試問題 2016年度 ( 平成28年度 )入試 算数1日目 5番 オイラーの関数 素数 互いに素 1000以下の整数のうち、2でも3でも5でも割り切れない整数を 小さいものから順に並べると 1,7,11,13,17,・・・・・・・,997 となります。 このなかで、一の位の数が7である整数は全部で□個あります。 また、7で割り切れる整数は全部で□個あります。 解き方 素数の楽しさを味わえる問題です 問題文の中に10以下の素数2,3,5,7が全て出てきています 2,3,5の最小公倍数は30ですから、1から30までの整数のなかで 2でも3でも5でも割り切れない整数を 書き出していきます でもここで、問題文のなかに 1,7,11,13,17というように17までは書いてくれています ここで灘の算数の問題は分かる人だけに分かるヒントが 問題文の中や例の中に隠されています 別に1,7,11,13,・・・・・・・,997というふうに問題分を書いても、 1,7,11,・・・・・・・,997と書いてもいいと思いませんか? それなのにどうして1,7,11,13,17というように17まで 書いてあるのでしょう? そのあと全部2,3,5で割り切れないことをチェックしていってもいいのですが、 13+17=30が使えることを知っている人だけに ちょっとでも有利になるように17まで書いてくれていると思います。 そこまで算数を楽しんでいる人を 灘が求めているのではないでしょうか? ここで灘中に上位合格する人たちが知っていることを 書いておきます ワンポイントアドバイス 13+17で30ですね あとは30-11で19 30-7で23 30-1で29となります(説明略) だからいっきに 1,7,11,13,17,19,23,29と書き出せます あとは30ごとに繰り返します 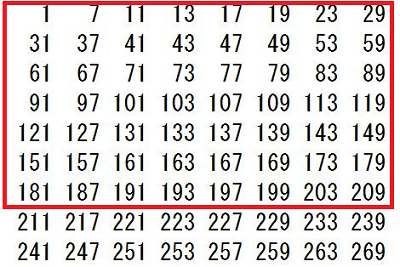 30までに一の位が7であるのは2つあります 1000÷30=33・・・10 2×33+1=67 灘中に上位合格する人たちは上の数表すべて書き出していません 前半の問題を解くのに 実際の試験上で計算用紙に書き出しているのは 最初の一行(1,7,11,13,17,19,23,29)で十分です 30ずつ繰り返すので、書かなくていいことが頭のなかでわかっています 30ずつ繰り返すことを意味も分からず、ただ覚えるのではなく、 理由を考えてみましょう。そうすると、 最初の一行で十分であることが理解できますね 最小公倍数のすごさ、素数のすごさ、繰り返すことのすごさを 感じられるのではないでしょうか つぎに後半の解き方ですが 30と7の最小公倍数は210ですので、 210までのなかで7で割り切れる整数をみつけます 上の表の赤枠の中で7の倍数は何個ありますか? これから受験の方は時間を計ってやってみましょう この作業がわりと時間がかかりますし、 計算ミスの可能性もありますね。 100までの7の倍数は普段練習しているので すぐに判定できると思います 100超えてからの7の倍数判定が時間がかかると思います 赤枠の中の4行目91を見つけてほっとしませんでしたか? これは一行に一つ7の倍数があるからあとは簡単と思ったら落とし穴に はまってしまいます 119も7の倍数ですよ 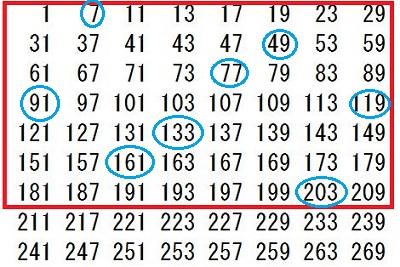 119が7の倍数であることを見つけても 121から209までの24個の整数全部を7で割るのはしんどいですよね? ここで違う思考回路を紹介します 使っている方も多いと思いますが 119が7の倍数とわかったら、そのことを活用するのです 7の倍数に7を足しても7の倍数ですね 頭のなかで126は表にないな 次は133これは表にある 140,147,154・・・・・・・という感じでやる方法です 時間がたっぷりあるときはもちろんどんな方法でもいいです これで赤枠の中に7の倍数が8個あることがわかりました 1000÷210=4・・・160 赤枠の中で160までの7の倍数は6個だから 8×4+6=38 これで答えは出ましたが、何か気づきませんでしたか? 赤枠をよ~く見てください 今度は縦に数字を見ていってください どの列にも7の倍数が1つずつありますね これは偶然ではないんですよ 理由がわかったらおそらく感動するかも 縦に見ていくということは30ずつ足していってますね 30を足すということは 30÷7=4・・・2 7で割った余りが2ですから 縦に2を加えていくと7で割った余りになります ということは、赤枠の中全部を7で割る必要がなくなります 最初の一行目(1,7,11,13,17,19,23,29)の整数を 7で割って余りを書き、縦に2を加えていく方法で 0になるところが、7の倍数です 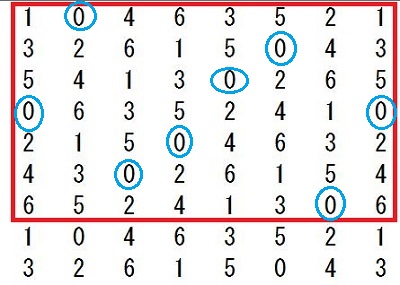 この方法だと大きな数を7で割るという作業をしていませんね だから後半の問題を速く正確に解けますね 問題を解くこととは関係ありませんが 表をよく眺めていると 赤枠の中のど真ん中を点対称の中心として 対応するところを足すと7で割り切れるようになっています 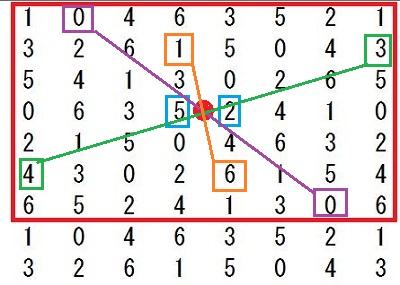 もう一度上の表を見ると、 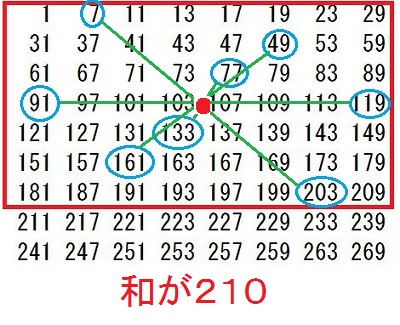 これってすごくないですか? 数の性質って美しいですね ここまで読んでくれたあなたに 最後に後半の問題を表を書き出さずに、 最初の一行(1,7,11,13,17,19,23,29)だけで解く方法を 紹介しておきます この8つの数をそれぞれ7倍してみてください そして、先程の上の表を見てください 先程がんばって探した7の倍数すべて (赤枠の中の青丸で囲んだ数)が 最初の一行(1,7,11,13,17,19,23,29)の7倍に なっていませんか? あまりの美しさに見惚れてしまいます ということは、本当に深く理解していたら、 最小公倍数210までに7の倍数が8個あることと 1000÷210=4・・・160 160÷7=22・・・6 最初の一行をみて、22までだから 1,7,11,13,17,19の6個 8×4+6=38 楽しんでいただけましたでしょうか 答え 順に 67 38 |
2022年度 東大寺学園中学 算数 2番(2) 整数 素数 素因数分解 実験 試行錯誤 整数を異なる3個の整数の積として表すことを考えます。 たとえば、24は、 1×2×12、 1×3×8、 1×4×6、 2×3×4 と4通りの表し方があります。 (ⅰ) 90を異なる3個の整数の積として表す方法は 全部で何通りありますか。 ただし、積の順序だけが異なるものは、 それらを全部で1通りとして数えます。 (ⅱ) 20以上の整数Aを、 異なる3個の整数の積として表すことはできず、 A+4も異なる3個の整数の積として表すことはできませんでした。 このような20以上の整数Aとして考えられるものを 小さいものから順に5個答えなさい。 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (ⅰ) 8 (ⅱ) 25,37,43,49,67 |
2022年度 東大寺学園中学 算数 4番 整数 場合の数 組合せ 実験 規則性 試行錯誤 整数Nに対して、Nの各位の数の和を S(N)と表します。たとえば、 S(7)=7 S(46)=4+6=10 S(1975)=1+9+7+5=22 です。 整数Nについて、次のような 【特性】 を考えます。 【特性】 NはS(N)で割り切れる。 たとえば、S(2022)=6で、2022÷6=337より、 2022は、S(2022)で割り切れます。 つまり、2022は 【特性】 をもちます。 このように、【特性】をもつ整数について、次の問いに答えなさい。 (1) 整数Nは【特性】をもち、1以上2022以下とします。 このような整数Nの中で、S(N)=5となるNは全部で何個ありますか。 (2) 整数Nは【特性】をもち、1以上2022以下とします。 このような整数Nの中で、S(N)=9となるNは全部で何個ありますか。 (3) 整数Nは【特性】をもち、1以上2022以下とします。 このような整数Nの中で、S(N)=18となるNは全部で何個ありますか。 (4) 整数Nは【特性】をもち、1以上2022以下とします。 S(N)の値として考えられるものの中で、 大きいものから3番目の値を求め、 そのときのNをすべて求めなさい。 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (1) 12 (2) 102 (3) 55 (4) S(N)=24 N=888,1896,1968 |
2022年度 東大寺学園中学 算数 1番 (1) 整数 規則性 実験 試行錯誤 (1) 1から200までの200個の整数を、 下のようにある規則に従って一列に並べました。 1,51,101,151,2,52,102,152,3,53,103,153,・・・ ・・・,48,98,148,198,49,99,149,199,50,100,150,200 (ⅰ) 123は左から何番目に並んでいますか。 (ⅱ) 連続して並んでいる4つの整数の和を計算したら323でした。 この4つの整数の中で最も左にある整数は、 列全体の左から何番目に並んでいますか。 答えはすぐに出せると思いますが、 答えにいたる途中過程を工夫すると あなただけのオリジナルな計算方法が発見されることもあり ほかの問題にもその同じ計算方法が使えて どんどん楽しくなりますよ 答 (ⅰ) 91 (ⅱ) 20 |
2022=337×2×3 337は素数です 337は素数です 奇素数337は2つの平方数の和で表される |
2023年度中学受験予定の方へ 2023=7×17×17 2023は素数ではありません 7や17や119や289などの倍数です 2000から2100までの素数は 2003,2011,2017,2027,2029, 2039,2053,2063,2069,2081, 2083,2087,2089,2099の14個あります
|
2017( 素数 )年中学入試予想問題はコチラ →2017年中学入試予想問題
おもしろ算数問題 2016年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2016年(中学入試)
おもしろ算数問題 2015年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2015年(中学入試)
おもしろ算数問題 50問(中学入試)にチャレンジはコチラ →おもしろ算数問題 50問(中学入試)
灘中学算数入試問題解説はコチラ → ■灘中学算数入試問題
2022年中学入試予想問題はコチラ →2022年中学入試予想問題
おもしろ算数問題 2022年(中学入試)にチャレンジはコチラ →おもしろ算数問題 2022年(中学入試)
■トップページ
■算数・数学スーパー個別指導のご案内
■灘中学算数入試問題
■おもしろ算数問題 50問(中学入試)
■お問い合わせ